第一作者简介:张陈明,男,安徽霍邱人,硕士,主检法医师,研究方向为法医物证学。E-mail: 448531970@qq.com
推导双祖疑母和双祖鉴定的平均非祖父母排除率( RGE)和祖孙关系指数( GI)公式,并对 RGE公式进行模拟实验验证。本研究首先根据双祖疑母(DGAM)和双祖(DG)鉴定的 RGE和 GI定义,分别推导 RGEDGAM、 GIDGAM和 RGEDG的数学公式,并依据15个STR基因座上的数据计算 RGEDGAM和 RGEDG的公式值。其次设计实验由15个STR基因座计算出 RGEDGAM和 RGEDG的模拟值。最后,将模拟值比对公式值,对所推导公式进行实验验证。结果表明, RGEDGAM和 RGEDG公式计算值与模拟实验验证值相符合。对比各类祖孙鉴定的 RGE,存在“双祖鉴定﹤双祖亲母鉴定﹤双组疑母鉴定”的规律。本文公式可应用于双祖疑母和双祖鉴定的 RGE和 GI计算。
The derivation was here carried out about the formulas of grandparent-plus-grandchild index ( GI) and average power of random grandparent exclusion ( RGE) under two conditions: indefiniteness of both double grandparents and mother; uncertainty of double grandparents, along with the resultant RGE formulas being empirically validated in principle. The formulas of RGE and GI were to derive on their own definition of indefiniteness of both double grandparents and mother ( RGEDGAM & GIDGAM) and uncertainty of double grandparents ( RGEDG). The derived formulas were to calculate into 15 STR loci from Identifiler kit. Furthermore, the simulated determination was to carry out about RGEDGAM, GIDGAM and RGEDG through multi-group operation with the same 15 STR loci. Finally, the formulas of RGEDGAM and RGEDG were to empirically validate in principle with correlation approach to the relevant values of formula and simulation. All the related formulas were thus derived, having those of RGEDGAM and RGEDG shown in accord with the simulation deliveries. For all the sorted RGEs relating to identification of grandparent and grandchild, there was an observation showing as RGEDG﹤ RGEDGBM (uncetain Double Grandparents yet certain Biological Mother, DGBM)﹤ RGEDGAM. The here-derived RGE and GI formulas are eligible to cope with the cases of indefiniteness of both double grandparents and mother and/or uncertainty of double grandparents.
时常有委托人要求运用STR检验鉴定疑似祖父母与被检孩子之间的亲缘关系, 即祖孙关系鉴定。在祖父母均参与的情况下, 祖孙鉴定有下列3种常见类型:
1)双祖亲母鉴定(double grandparents and biological mother, DGBM), 指已知母亲为孩子生母, 鉴定祖父母是否为孩子的亲生祖父母; 2)双祖疑母鉴定(double grandparents and alleged mother, DGAM), 指祖父母与孩子的关系未知, 母亲与孩子关系也未知, 同时鉴定祖父母和母亲是否为孩子的亲生祖父母和生母; 3)双祖鉴定(double grandparents, DG), 指鉴定祖父母是否为孩子的亲生祖父母。其中双祖亲母和双祖鉴定多见于司法鉴定, 双祖疑母鉴定多见于公安机关的灾难事件、拐卖失踪和无名尸体等案件鉴定。《生物学祖孙鉴定规范》[1]已提供双祖亲母鉴定的祖孙关系指数(grandparent index, GI)和平均非祖父母排除率(average/mean power of random grandparent exclusion, RGE)公式, 柳燕等[2]报道了双祖鉴定的GI公式, 任贺等[3] 报道了单亲隔代亲权指数计算方法。但双祖疑母鉴定的GI和RGE公式以及双祖鉴定的RGE公式未见报道。本文尝试对此提出相应概念和数学推导公式, 并设计模拟实验验证。
符合祖孙关系判断标准为:孩子的一对等位基因必定是其中一个来自母亲, 另一个来自祖父或祖母。参照《生物学祖孙鉴定规范》, 在双祖疑母鉴定和双祖鉴定中, 分别定义RGE和GI如下:
1)双祖疑母鉴定的平均非祖父母排除率(RGEDGAM)指在单基因座上, 随机祖父母、随机母与随机孩子排除祖孙关系的概率。
2)双祖疑母鉴定的祖孙关系指数(GIDGAM)指在单基因座上, 争议祖父母、争议母与孩子之间符合祖孙关系时其遗传表型出现的概率(X)与争议祖父母、争议母与孩子是无关个体时其遗传表型出现的概率(Y)比值。
3)双祖鉴定的平均非祖父母排除率(RGEDG)指在单基因座上, 随机祖父、随机祖母与随机孩子排除祖孙关系的概率。
公用设定:在某基因座上, 等位基因有n个, i, j∈ [1, n], i﹤j。等位基因A1~An的对应的基因频率为P1~Pn。
1.2.1 RGEDGAM公式推导(表1)
| 表1 RGEDGAM公式推导 Table 1 Derivation of RGEDGAM |
设Ar代表所有等位基因, 则Pr=1。设As代表除Ai以外的所有等位基因, 则Ps=1-Pi。设At代表除Aj以外的所有等位基因, 则Pt=1-Pj。设Au代表除Ai和Aj以外的所有等位基因, 则Pu=1-Pi-Pj。参照双亲皆疑排除率公式推导[4, 5], 将祖父和祖母视为有4个等位基因的特殊父亲。
1)当祖父母无Ai, 疑母任意时, 排除与孩子AiAi的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=Pi2(1-Pi)4。
2)当祖父母任意, 疑母无Ai时, 排除与孩子AiAi的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=Pi2(1-Pi)2。
其中1)和2)均将“ 祖父母无Ai且母无Ai” 的情况计入, 必须去除重复。重复的合并概率=子概率× 母概率× 祖父母排除概率=Pi2(1-Pi)6。
3)当祖父母无Aj, 疑母为AiAi时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=2Pi3Pj(1-Pj)4。
4)当祖父母无Ai, 疑母为AjAj时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=2PiPj3(1-Pi)4。
5)当祖父母无Ai且无Aj, 疑母为AiAj时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=4Pi2Pj2(1-Pi-Pj)4。
6)当祖父母无Aj, 疑母有Ai无Aj时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=4Pi2Pj(1-Pi-Pj)(1-Pj)4。
7)当祖父母无Aj, 疑母有Aj无Ai时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=4PiPj2(1-Pi-Pj)(1-Pi)4。
8)当祖父母任意, 疑母无Ai且无Aj时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 母概率× 祖父母排除概率=2PiPj(1-Pi-Pj)2。
综上推导, RGEDGAM公式为:
$\begin{array}{l} R G E_{\mathrm{DOMM}}=\sum_{i=1}^{n} P_{i}^{2}\left(1-P_{i}\right)^{2}\left[1+\left(1-P_{i}\right)^{2}-\left(1-P_{i}\right)^{4}\right]+\sum_{i< j}^{n} 2 P_{i} P_{j}\left[P_{i}^{2}\left(1-P_{j}\right)^{4}+P_{j}^{2}\left(1-P_{i}\right)^{4}\right]+ \\ \sum_{i< j}^{n} 4 P_{i} P_{j}\left(1-P_{i}-P_{j}\right)\left[P_{i}\left(1-P_{j}\right)^{4}+P_{j}\left(1-P_{i}\right)^{4}\right]+\sum_{i< j}^{n} 2 P_{i} P_{j}\left(1-P_{i}-P_{j}\right)^{2}\left[1+2 P_{i} P_{j}\left(1-P_{i}-P_{j}\right)^{2}\right] \end{array}$ (1)
1.2.2 GIDGAM公式推导(表2)
| 表2 GIDGAM公式推导 Table 2 Derivation of GIDGAM |
设等位基因A、B的基因频率分别为a、b。设等位基因C代表非A的等位基因, 等位基因D代表非A且非B的等位基因。设自然数m、n, 1≤ m≤ 4, 1≤ n≤ 4。为简化公式, 将祖父× 祖母基因型描述为基因型集合的形式, 分为以下3种:
1)含m个A基因的基因型集合。
a. 含1个A基因的基因型集合={AC× CC, CC× AC}。
b. 含2个A基因的基因型集合={AA× CC, CC× AA, AC× AC}。
c. 含3个A基因的基因型集合={AA× AC, AC× AA}。
d. 含4个A基因的基因型集合={AA× AA}。
2)含m个A或B基因的基因型集合, 代表基因型集合中的A基因个数与B基因个数之和为m个, 其中A基因或B基因的个数可以为0。
a. 含1个A或B基因的基因型集合={AD× DD, DD× AD, BD× DD, DD× BD}。
b. 含2个A或B基因的基因型集合={AA× DD, DD× AA, AD× AD, BB× DD, DD× BB, BD× BD, AB× DD, DD× AB, AD× BD, BD× AD}。
c. 含3个A或B基因的基因型集合={AA× AD, AD× AA, BB× BD, BD× BB, AA× BD, BD× AA, AB× AD, AD× AB, BB× AD, AD× BB, BA× BD, BD× BA}。
d. 含4个A或B基因的基因型集合={AA× AA, BB× BB, AB× BB, BB× AB, AA× AB, AB× AA, AB× AB, AA× BB, BB× AA}。
3)含m个A或B基因的基因型集合, 代表基因型集合中的A基因个数与B基因个数之和为m个。例如:含2个A基因和1个B基因的基因型集合={AA× BC, BC× AA, AB× AC, AC× AB, CA× AB, AA× DB, AB× DA, AB× AD, AA× BD, BD× AA}。
参照双亲皆疑亲权指数[5]和三联体亲权指数公式推导[6], 将祖父和祖母视为有4个等位基因的特殊父亲, 进行GIDGAM公式推导。
1.2.3 RGEDG公式推导
参照二联体非父排除率公式推导[7], 将祖父和祖母视为有4个等位基因的特殊父亲。根据孩子基因型分2种类型:
1)当祖父母无Ai时, 排除与孩子AiAi的亲生关系。合并概率=子概率× 祖父母排除概率= Pi2(1-Pi)4。
2)当祖父母无Ai且无Aj时, 排除与孩子AiAj的亲生关系。合并概率=子概率× 祖父母排除概率=2PiPj(1-Pi-Pj)4。
综上, RGEDG公式为:
$R G E_{\mathrm{DG}}=\sum_{i=1}^{n} P_{i}^{2}\left(1-P_{i}\right)^{4}+\sum_{i< j}^{n} 2 P_{i} P_{j}\left(1-P_{i}-P_{j}\right)^{4} $ (2)
1.3.1 模拟随机样本
根据随机模拟法[5]产生Identifiler试剂盒的15个常染色体STR基因座的模拟随机个体, 等位基因的概率参考中国汉族人群基因频率[8]。设S为单基因座的所有等位基因频率之和, 则S=∑ Pi[9]。对以上中国汉族人群基因频率计算后发现, 只有D16S539、D2S1338、FGA、TPOX基因座的S=1, 其他11个基因座的S≠ 1。因此对11个S≠ 1的基因座进行基因频率微调, 确保全部基因座的S=1, 并以此作为模拟实验的基础频率。
1.3.2 模拟实验设计
在单基因座上产生1 000万组, 每组包含4个模拟随机个体, 分别视为祖父、祖母、疑母和孩子, 分别在每组中判断祖父母、疑母和孩子是否符合祖孙关系。设RGEDGAM模拟值(RGEDGAM-S)=不符合祖孙关系的组数/总组数, 分别计算各基因座的RGEDGAM-S。根据公式(1)计算各基因座RGEDGAM公式值(RGEDGAM-F), 与RGEDGAM-S进行对比。
在单基因座上产生1 000万组, 每组包含3个模拟随机个体, 分别视为祖父、祖母和孩子, 分别在每组中判断祖父母和孩子是否符合祖孙关系。设RGEDG模拟值(RGEDG-S)=不符合祖孙关系的组数/总组数, 分别计算各基因座RGEDG-S。根据公式(2)计算各基因座RGEDG公式值(RGEDG-F), 与RGEDG-S进行对比。
基于本文微调后中国汉族人群基因频率, 15个基因座的RGEDGAM-F、RGEDGAM-S、RGEDG-F、RGEDG-S对比见表3。
| 表3 15个STR基因座的RGE和PE对比 Table 3 Comparison of both RGE and PE calculated from 15 STR loci of Identifiler kit |
为了对比其他鉴定, 基于同样基因频率计算二联体非父排除率(PEduo)、三联体非父排除率(PEtrio)、双亲皆疑排除率(PEAP)、双祖亲母鉴定的平均非祖父母排除率(RGEDGBM)列入表3。
对RGEDGAM的公式值和模拟值绘制散点图, 见图1。以SPSS 19.0进行线性回归分析, 得R2=1, P< 0.001。分析表明各基因座的RGEDGAM的公式值和模拟值结果一致, 公式(1)符合模拟实验验证。
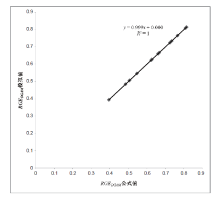 | 图1 RGEDGAM公式值与模拟值的直线回归分析Fig. 1 Linear regression analysis of RGEDGAM with its formula values versus simulation ones |
对RGEDG的公式值和模拟值绘制散点图, 见图2。以SPSS 19.0进行线性回归分析, 检验得R2=1, P< 0.001。分析表明各基因座的RGEDG的公式值和模拟值结果一致, 公式(2)符合模拟实验验证。
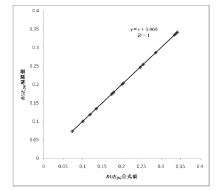 | 图2 RGEDG公式值与模拟值的直线回归分析Fig. 2 Linear regression analysis of RGEDG with its formula values versus simulation ones |
对比各基因座3个祖孙鉴定的RGE公式值发现, RGEDG< RGEDGBM< RGEDGAM。因此祖孙鉴定的RGE存在如下规律:双祖鉴定< 双祖亲母鉴定< 双祖疑母鉴定。进一步将各基因座的祖孙鉴定RGE与二联体、三联体、双亲皆疑鉴定PE对比, 发现如下规律:双祖鉴定< 双祖亲母鉴定< 二联体鉴定< 三联体鉴定< 双祖疑母鉴定< 双亲皆疑鉴定。
祖父母均参与的祖孙鉴定不仅常见于司法鉴定实践中, 而且在大型灾难、打拐寻亲、失踪人口中对受害者的身份识别也具有重要的实战应用价值。本文基于规范所定的双祖亲母鉴定的RGE和GI公式, 结合数学推导和模拟验证, 补充了双祖疑母鉴定和双祖鉴定的概率计算方法, 对于祖孙鉴定应具有法医学应用价值。特别是双祖鉴定, 因为其中没有母亲参与, 不能运用母子二联体鉴定, 是司法鉴定中亟待解决的问题之一。
本文借鉴双亲皆疑排除率和亲权指数、二联体非父排除率的公式推导方法, 将祖父和祖母视为有4个等位基因的特殊父亲, 获得双祖疑母鉴定RGE和GI、双祖鉴定RGE公式。在此条件下, 本文祖孙鉴定的3个分类与经典亲子鉴定(即二联体/三联体/双亲皆疑鉴定)的3个分类可以建立一一对应关系。将祖父母对应父亲, 则双祖亲母鉴定对应三联体鉴定, 双祖疑母鉴定对应双亲皆疑鉴定, 双祖鉴定对应二联体鉴定。祖孙鉴定与经典亲子鉴定, 其定义和判别原理十分相似, 可视为4个等位基因父亲参与下的特殊经典亲子鉴定。将有对应关系的祖孙鉴定和经典亲子鉴定进行逐一对比(双祖对应二联体, 双祖亲母对应三联体, 双祖疑母对应双亲皆疑), 可见前者的排除率明显低于后者。考虑到对应的祖孙鉴定比经典亲子鉴定多发生了一次等位基因遗传, 增加了很多不确定因素, 因此祖孙鉴定鉴别能力相对较低也是符合理论预期的。
已报道的双祖亲母和双祖鉴定的GI公式均属于部分举例公式, 主要问题是未能穷举所有可能的祖父母基因型组合。笔者参照上文双祖疑母GI公式对祖父母基因型的描述, 将双祖亲母GI(GIDGBM)和双祖GI(GIDG)公式写为全覆盖的数学公式(见表4和表5), 以利于人工或软件计算。本文GI公式未考虑基因突变情形, 当需要时可参照规范中的举例公式, 进一步推导3种祖孙鉴定的突变计算方法。
| 表4 GIDGBM公式 Table 4 Formulae of GIDGBM |
| 表5 GIDG公式 Table 5 Formulae of GIDG |
对于祖父母均参与的祖孙鉴定案例, 应可推定:
1)同样适用于外祖父母和孩子的鉴定, 根据父亲参与情况分为生父、疑父和缺父3种类型, 可直接套用本文的分类方法和计算方法。
2)尽可能让母亲参与鉴定, 因为有母亲的RGE(双祖亲母/双祖疑母)大大高于无母亲的RGE(双祖), 此不仅意味着鉴别能力高, 而且GI值也能大大提高。
3)如有必要, 可补充Y-STR或X-STR检验, 以进一步降低风险。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|


