加权保真与稀疏约束的混合噪声鲁棒人脸超分辨率算法
[吴文强
, 唐松泽* ]
, 唐松泽]
引用本文
吴文强, 唐松泽. 加权保真与稀疏约束的混合噪声鲁棒人脸超分辨率算法[J].刑事技术, 2022,47(4):356-363
WU Wenqiang, TANG Songze. A Super-resulution Algorithm Enhancing Robustness of Noise-mixed Human Face via Weighted Fidelity and Sparse Constraint[J]. Forensic Science and Technology,2022,47(4): 356-363
Doi: 10.16467/j.1008-3650.2022.0012
WU Wenqiang, TANG Songze. A Super-resulution Algorithm Enhancing Robustness of Noise-mixed Human Face via Weighted Fidelity and Sparse Constraint[J]. Forensic Science and Technology,2022,47(4): 356-363
Permissions
Copyright©2022, 《刑事技术》编辑部
《刑事技术》编辑部
加权保真与稀疏约束的混合噪声鲁棒人脸超分辨率算法
第一作者简介：吴文强,男,江苏高邮人,硕士,工程师,研究方向为图像处理。E-mail: 289373480@qq.com
摘要
目的 当人脸图像受到混合噪声（典型的如加性高斯白噪声和脉冲噪声混合）污染时,生成高分辨率人脸就成了一项具有挑战性的任务。本文拟针对这一问题,提出一种基于加权保真和稀疏约束的鲁棒人脸超分辨率算法。方法 在数据保真项中引入加权矩阵来准确表征重建剩余残差的分布。此外,为了稳定最优权值,引入表示系数的稀疏先验作为正则项。最后,将加权重建残差和表示系数的稀疏约束统一到变分框架中,该变分框架在抑制混合噪声干扰的同时,获取高分辨率的人脸图像。结果 在公共人脸数据库FEI上进行了对比实验,结果表明,在峰值信噪比、结构相似性度量等方面本文算法均优于现有的人脸超分辨率方法。结论 该算法能有效抑制图像中的混合噪声,且能恢复出足够多的细节,验证了加权与稀疏约束在混合噪声干扰下实现人脸图像超分辨率的可行性。
关键词:
人脸图像; 混合噪声; 加权矩阵; 邻域嵌入; 稀疏表示; 鲁棒性; 超分辨率
中图分类号:DF793.2
文献标志码:A
文章编号:1008-3650(2022)04-0356-08
A Super-resulution Algorithm Enhancing Robustness of Noise-mixed Human Face via Weighted Fidelity and Sparse Constraint
Abstract
Face hallucination, a technique that is able to reconstruct high-resolution (HR) faces from low-resolution (LR) ones, makes it come true through the prior knowledge learned from HR/LR face pairs. Most state-of-the-art manipulations leverage the position-patch prior knowledge of human face to estimate the optimal representation coefficients for each image patch. However, the majority of existing approaches only operates eligibly in noise-free or single camera/atmospheric noise (i.e., Gaussian or impulse) situations. With the facial images suffering from mixed noise (typical as additive white Gaussian noise: AWGN and impulse noise: IN), a super-resolution face becomes challenging for realization. To address this problem, a novel algorithm of face hallucination was here proposed on the basis of weighted fidelity and sparse constriant. The traditional fidelity definition can not accurately calculate the reconstructive residual under interference of noises. To characterize the distribution of reconstructive residuals well, a weighted matrix was therefore introduced into a data-fidelity term. Besides, given that only a limited number of reconstructive weights will have a positive impact on the reconstruction results, the sparse prior of representation coefficients was to stabilize the optimal weights as a regularization term. In addition, the weighted reconstructive residuals and the sparsity of representation coefficients were unified into a variational framework, therewith helping suppress the mixed noise and achieve the optimal hallucinated face images simultaneously. To demonstrate the effectiveness of this handling, a comparison was carried out with the here-proposed method against the other state-of-the-art approaches on public FEI face database. The experimental results showed that the proposed algorithm gave better performance than the other existing face hallucination choices on peak signal noise ratio (PSNR) and structural similarity index (SSIM). Combined with the strengths of weighted reconstructive residuals and the sparsely-constrained representation, a considerable improvement was achieved over several existing state-of-the-art face hallucination models quantitatively and qualitatively. The simulation experiments verified that our proposed method can effectively suppress the mixed noise and recover enough details. Furthermore, a desired result was obtained with the frontal face or near-frontal face being as the training set. Nevertheless, when the monitored image was a low-light or non-frontal pose, the hallucination results were not good commonly. Imaginarily, were a transformation model to pre-construct to map the training set with an arbitrary pose onto a frontal face set, a good performance would be derived expectantly. In fact, thanks to the facility of getting a sequence of face images in actual monitoring environment, the residual face information from the sequence, as an important prior, will be good item helping to recover a face image of high quality and resolution.
Key words:
face image; mixed noise; weighted matrix; neighbor embedding; sparse representation; robustness; super-resolution
在公安工作中, 犯罪嫌疑人的高分辨率（high resolution, HR）面部图像是非常重要的线索。然而现实中, 相机或传感器捕捉到的一般均是低分辨率（low resolution, LR）图像, 这其中主要受到包括相机模糊、物体与成像系统的距离、噪声等各种因素的影响, 因此, 研究从观察获取到的低分辨率图像中恢复出其对应的高分辨率图像具有重要意义[1, 2, 3, 4]。围绕它, 学者们提出了一系列的算法模型, 大致可以分为两大类：1）基于全局图像的人脸超分辨率方法; 2）基于局部图像块的人脸超分辨率方法。
为了实现全局图像的人脸超分辨率, 几种典型的特征提取方法被用于抽取图像的相关特征, 如主成分分析（principal component analysis, PCA）[5]、局部保持投影（loality preserving projection, LPP）[6]和典型相关分析（canonical correlation analysis, CCA）[7]。Wang等[8]通过PCA将输入的低分辨率图像分解为一组低分辨率样本人脸图像和一组系数的线性组合, 再根据得到的系数由相应的高分辨率样本人脸图像生成高分辨率人脸。Chakrabarti等[9]在高维图像空间中, 利用核PCA（Kernel PCA）模型对人脸图像进行处理。与保持线性全局结构的PCA相比, LPP可以揭示非线性特征, Zhang等[10]在LPP子空间中自适应地选取样本, 有效地恢复了LR人脸图像中丢失的高频成分。Huang等[7]利用典型相关分析建立了相干空间中低分辨率图像和高分辨率图像之间的非线性映射模型。该方法先将人脸图像转换为一维向量空间, 这破坏了图像的拓扑结构。因此, An[11]将CCA的思想进一步扩展到二维空间, 提升了算法的性能。这些全局方法虽然取得了很好的效果, 但图像中的细节（如边缘或纹理信息）无法得到保留。
图像块是将整幅人脸图像按重叠像素分割得到的。Chang等[12]首次基于局部线性嵌入（locally linear embedding, LLE）[13]的思想建立了邻域嵌入（neighbor embedding, NE）的超分辨模型, 该模型假设低分辨率图像块流形与高分辨率图像块流形具有相同的拓扑结构。人脸作为一种高度结构化的图像, 其图像块位置信息是形成高分辨率图像的重要先验。Ma等[14]提出了一种利用人脸图像块位置先验信息估计最优权值的最小二乘表示（least square regression, LSR）方法。在该模型中, 根据低分辨率样本脸图像块的位置, 计算出每一测试低分辨率图像块的最优重建权重。
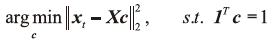
其中xt是从输入的LR人脸图像中提取的图像块。X=[x1, x2, …, xN]表示训练集中位于同一位置的所有图像块集合。xt是训练集X和重建权重c=[c1, c2, …, cN]T的线性组合。一般情况下, 通过最小化重构残差可以得到最优的权重。但当测试块的维数小于训练样本的大小时, LSR方法常常生成非唯一的权重。因此, 需要额外的正则化项来约束不适定问题的求解[15, 16, 17, 18, 19, 20]。基于以上分析, 重建权重的稀疏性作为正则化项提升了超分辨率的性能[16, 17]。与稀疏性相比, 局部性先验在揭示非线性流形的几何结构方面也很重要, Jiang等[19]将局部约束先验引入人脸超分辨率中并取得了很好的效果。为了同时实现局部性和稀疏性约束, 文献[20]提出了Tikhonov正则化邻域表示方法（Tikhonov regularization neighbor embedding, TRNR）。上述方法在无噪声或含加性高斯白噪声（additive white Gaussian noise, AWGN）条件下对于LR人脸图像可以明显提升其分辨率。由于实际成像环境复杂, 脉冲噪声也是常见的图像退化类型[21, 22, 23, 24, 25, 26]。鲁棒局部约束双层表示（robust face hallucination via locality-constrained bi-layer representation, RLcBR）模型被用于超分辨率被脉冲噪声破坏的人脸图像[25]。最近, 为了解决混合噪声（加性高斯白噪声和脉冲噪声）, 一种基于误差收缩最近邻表示（error shrunk nearest neighbors representation, ESNNR）的人脸超分辨率方法被提出来[26], 该方法基于局部信息先验的阈值法识别LR人脸图像中的高动态内容, 再抑制识别出的高动态内容, 实现重建误差最小化。多特征分层学习模型（multiple feature learning with hierarchical structure, MLHS）[27]充分利用了人脸图像信息的多层次特点, 采用层次结构来更好地维护HR和LR图像空间之间的流形一致性假设。Nagar等[28]提出了基于残差学习的误差抑制最近邻表示方法（residual learning-based error suppressed nearest neighbor representation, RLENR）, 该方法首先利用面向PCA的匹配面抑制LR人脸图像中的脉冲噪声, 然后通过引入残差学习来更新LR训练集, 使高斯噪声的影响最小化, 最后, 利用更新后的LR训练集生成输入的LR人脸细节。
目前的研究方法均有一个前提, 即不同类型噪声下的重建残差（xt-Xc）是基于L2-范数建模的。然而, 如图1所示, 在混合噪声情况下, 重建残差的分布通常偏离正态分布（尤其在尾部）。为了解决上述问题, 本文引入加权矩阵来自适应缩小重建残差以符合高斯分布。此外, 本文还引入了表示重建权重的稀疏先验项, 最终将加权的L2-范数与L1-范数统一到一个变分框架中。本文的主要创新之处如下：
 | 图1 噪声图像分布的比较（a：混合噪声（高斯噪声和椒盐噪声）污染的图像; b：不同类型噪声的残差分布; c：b在对数域中的表示; d：加权残差和高斯分布在对数域中的分布）Fig.1 Distribution of noise in a facial image (a: a corrupted image by mixed noises: Gaussian noise and Salt & Pepper noise; b: the distribution of $||x_{t}-Xc||^{2}_{2}$ (residual) under different types of noises. c: representation of b in log domain; d: the distribution of both weighted residual and Gaussian fitting in log domain) |
1）不同于之前研究对所有像素用不变的方式处理, 本算法利用加权矩阵自适应地调整每个像素的重建残差以抑制混合噪声的影响, 获得最优的重构权重来合成高分辨率的人脸图像。
2）为了提高模型解的稳定性, 将权重系数的稀疏先验引入模型中。这使得本算法能够在系数的表示空间中维持其拓扑结构的一致性。
3）与传统方法先去噪声再超分辨率不同, 本算法通过一个统一的变分框架, 同时实现混合噪声去除和对输入的LR人脸图像实现分辨率提升。
1 方法
1.1 符号表示
在训练集中, 有N对的高-低分辨率的人脸图像, 记IH={I1H, I2H, …, INH}为高分辨率人脸图像样本集, IH={I1L, I2L, …, INL}为对应的低分辨率人脸图像样本集。每幅高-低分辨率的人脸图像被划分为M=AB个重叠的图像块, 并分别表示为：
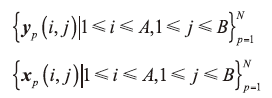
输入的低分辨率测试人脸图像也用同样的划分方式表示为：
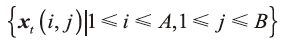
估计出相应的高分辨率图像块：
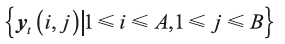
最后, 根据yt(i, y)的位置(i, y), 将所有的高分辨率图像块进行整合得到高分辨率人脸像到ItH。为了方便起见, 在接下来的表述中省略(i, y)。混合噪声中脉冲噪声（椒盐噪声）密度为“ ζ ” , 加性高斯白噪声的标准差为“ σ ” 。
1.2 模型设计
如前所述, 之前的研究工作是基于一个共同的假设：不同类型噪声下的重建残差（xt-Xc）可以用L2范数建模。基于L2范数的数据保真项设计, 使得模型可以有闭合解。然而实际的视频监控系统, 观测到的人脸图像往往会受到混合噪声（如高斯噪声和脉冲噪声的混合, 如图1a所示）的影响, 重建残差的分布一般与高斯分布不同, 如图1b所示。因此, 用简单的L2范数来刻画数据拟合残差并不是最优的。为此, 可以在重建残差中引入一个加权矩阵, 为每个残差分配合适的权重, 自适应地衡量每个像素的损失程度, 如图1d所示。
根据以上分析, 设计一个新的加权数据保真项, 从而建立一个混合噪声下的人脸超分辨率新模型。
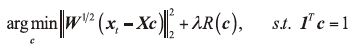
其中W是对角线权重矩阵, 对角线元素Wii=wi。R(c)表示正则化项, 参数λ 平衡数据保真度项和正则化项。
由于训练集X的固定性, 可以在最大后验概率（maximum a posteriori, MAP）框架下计算表示系数
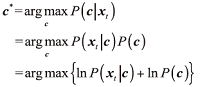
似然项的特征P(xt|c)服从高斯分布。因此有
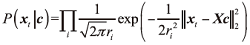
式中rj是xt-Xc的标准差。
对于权重向量c, 其概率分布p(c)用Lp范数刻画
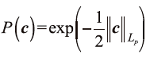
式中||· ||Lp是Lp范数。由公式(3)~(5)推导出
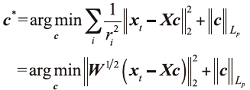
因此, 对角线元素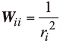 
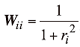
加权重建残差是在图像块空间中数据保真, 在重建权重系数的表示空间需要揭示其分布的特征。
$min||x_{t}-Xc||^{2}_{2}$表明在原始数据空间中, 相似的图像块具有相似的拓扑结构。进一步扩展到在表示空间中构造关于重建权重系数c的类似关系, 则在局部有相似性关系如下：
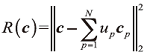
式中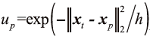 
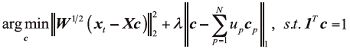
1.3 模型求解
为了简化表述模型, 记 
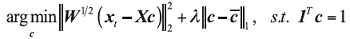
首先将对角矩阵D初始化为单位矩阵, 然后在第k+1次迭代中, D中的每个元素更新为
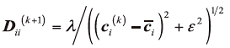
式中：ε 是标量, ci(k)表示第k步迭代的权重向量c的第i个元素, 接下来, 更新c
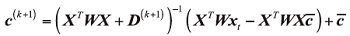
如此循环更新D和c, 直到得到最佳的c。提出的人脸超分辨率过程见补充材料算法S1。
2 实验结果与分析
2.1 人脸库介绍
所有的模拟实验均在FEI人脸库[30]上进行。该数据库有200个人的400张面部图像, 所有的图像都被对齐并被裁剪成30× 25个像素作为高分辨率训练图像。在生成LR人脸训练图像时, 对相应的高分辨率训练图像进行平滑处理, 并按4倍进行下采样, 然后加入不同级别的混合噪声。在模拟实验中, 随机抽取180个人共360幅图像进行训练, 其余样本进行测试。
2.2 参数分析
将研究正则化参数λ 、图像块大小与重叠像素个数、迭代次数对算法的影响。
2.2.1 不同λ 下的结果
从公式（8）可知λ 用于平衡稀疏约束和加权重建残差以取得最优性能。
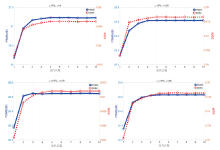
图2根据不同的λ 值绘制了不同噪声水平下的平均峰值信噪比（peak signal-to-noise ratio, PSNR）和结构相似性指数度量（structural similarity index measure, SSIM）的变化曲线。随着λ 的增大（0< λ < 210）, 该方法的客观评价指标PSNR和SSIM将增大。这说明稀疏约束在面片表示中起着积极的作用。但λ 的值不能设置得太高（λ > 210）。当λ 在210左右时, 提出的算法可以获得稳定和最佳的性能。因此, 在接下来的实验中设置λ =210。
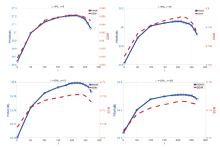 | 图2 不同噪声水平下λ 值对超分辨率结果的影响Fig.2 The effect of different regularization parameters λ under various noise levels |
2.2.2 不同图像块大小与重叠像素个数下的结果
在基于图像块的人脸超分辨率方法中, 图像块大小和重叠像素对最终的结果起着重要的作用。图3显示了在FEI数据库中, 不同图像块大小和重叠像素的量化性能（PSNR和SSIM）。通过对比分析, 可以得出以下结论：
 | 图3 不同噪声水平下图像块大小（横坐标括号中第一个数字）和重叠像素（横坐标括号中第二个数字）对PSNR和SSIM的影响Fig.3 Effect of different patch sizes (the first number in parentheses on the abscissa) and overlapping pixels (the second number in parentheses on the abscissa) on the average PSNR and SSIM scores under various noise levels |
1）图像块的大小影响最终的合成性能。选择合适大小的图像块可以很好地保留面部结构信息和细节。
2）在图像块大小固定的情况下, 随着重叠像素的增加, 超分辨率的性能也会提高。然而, 重叠像素的增加也需要更多的计算时间。最后, 折衷考虑性能与计算时间, 图像块大小设置为20、重叠像素为12。
2.2.3 不同迭代次数的结果
为了测试迭代次数对超分辨率结果的影响, 绘制了不同迭代次数下PSNR和SSIM平均值变化曲线, 如图4所示。结果表明, 随着迭代次数的增加, 提出的算法具有较好的一致性和稳定性, 即在大多数情况下, 经过5次迭代, 算法可以快速收敛到满意的结果, 这也意味着提出的算法在现实中可以推广应用。
 | 图4 不同迭代次数下PSNR和SSIM性能Fig.4 The performance of PSNR and SSIM obtained from different iteration times |
2.3 混合噪声下算法鲁棒性测试
为了测试提出的人脸超分辨率算法的鲁棒性、优越性, 对输入的LR人脸图像加入不同水平的混合噪声, 再用LSR[14]、TRNR[20]、RLcBR[25]、ESNNR[26]、MLHS[27]方法以及一种基于深度学习的方法SRGAN （super-resolution using a generative adversarial network）[31]进行了定性和定量的比较。由于这些比较方法对异常值不具有鲁棒性, 实验首先使用自适应中值滤波器（adaptive median filter, AMF）[32]对原始输入含噪声低分辨率图像进行处理, 以减少异常值对结果的影响。不同混合噪声下各类方法的PSNR和SSIM平均值见补充材料表S1。
实验表明, 本文提出的算法在大多数情况下都优于其他5种方法。为了便于视觉比较, 补充材料图S1展示了部分结果。显然, 由本文所提出方法恢复的图像有较少的噪声和伪影, 并且更好地保留细节和纹理。由于缺少关于脸部图像的一些先验信息, LSR方法生成的图像有严重的可见伪影（参见图S2第2列）。TRNR方法的输出仍有一些噪声（参见图S2第3列）。RLcBR方法的性能取决于AMF检测脉冲噪声的精度, 然而, 在混合噪声情况下, 很难准确地识别噪声的性质。因此, 当高斯噪声在混合噪声中的贡献很小时, RLcBR方法给出了很好的结果, 而随着高斯噪声水平的增大, RLcBR方法的性能明显下降。ESNNR方法通过误差收缩技术将识别出的高动态内容（如离群值或噪声）减小并引导重建, 但对于尖锐的边缘也会进行抑制。MLHS方法随着混合噪声水平的增大显示出不鲁棒的性能。RLENR方法在第一阶段用PCA方法抑制脉冲噪声, 但与此同时也忽视了人脸的细节信息, 所以在脉冲噪声增强的情况下性能下降比较明显。目前, 基于深度学习的方法在图像恢复等许多领域都取得了令人瞩目的效果。遗憾的是, SRGAN方法在噪声场景下并没有达到令人满意的超分辨率性能, 它的输出受到异常值的严重影响。尽管在只有脉冲噪声（σ =0）的情况下, 本文算法在客观性度量指标上表现一般, 但在视觉效果上与最好的算法没有明显区别。混合噪声情况下, 与六个有代表性的方法相比, 本文提出的方法在视觉效果上表现更佳, 在大部分情况下均表现出了优秀的结果。
3 结论
针对人脸超分辨率过程中混合噪声（高斯噪声和椒盐噪声）的影响, 提出了利用加权数据保真项和表示系数的稀疏正则化的重建模型。在混合噪声下, 重建残差的分布不同于传统的高斯分布, 为此引入一个加权矩阵来自适应处理混合噪声下的像素。另外, 通过理论推导出图像块表示的先验性, 提出利用L1范数来刻画重建系数的权重。最终实验验证了本文提出的超分辨率方法对人脸图像中的混合噪声能有效抑制, 且可以恢复出足够多的细节, 也直接验证了加权与稀疏约束在混合噪声干扰下实现人脸图像超分辨率的可行性。
补充材料
与本文相关的补充数据见：http://www.xsjs-cifs.com/CN/abstract/abstract6988.shtml。
参考文献
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|