引用本文
鲍立垠, 李轶昳, 张雯, 崔斌, 金益锋, 马新和. 称重计数法计算气枪弹检材数量[J].刑事技术, 2018,43(6):436-440
BAO Liyin, LI Yiyi, ZHANG Wen, CUI Bin, JIN Yifeng, MA Xinhe. Weighing to Count the Quantity of Air Gun Pellets[J]. Forensic Science and Technology,2018,43(6): 436-440  
Doi: 10.16467/j.1008-3650.2018.06.002
Permissions
Copyright©2018, 《刑事技术》编辑部
《刑事技术》编辑部
称重计数法计算气枪弹检材数量
鲍立垠1, 李轶昳1, 张雯2, 崔斌1,*, 金益锋1, 马新和1
1.公安部物证鉴定中心,北京100038
2.燕山大学环境与化学工程学院,河北 秦皇岛 066004
* 通讯作者：崔斌（1989—）,男,山西孝义人,硕士,研究实习员,研究方向为涉枪物证检验鉴定。E-mail：ccuibinn@126.com

第一作者简介：鲍立垠（1986—）,男,江西南昌人,博士,副研究员。研究方向为涉枪物证检验鉴定、物证鉴定质量控制。 #现在阿里巴巴集团安全部工作（杭州,311121）。E-mail：boilingbao@163.com

基金资助: 证据科学教育部重点实验室（中国政法大学）开放基金资助课题（No.2018KFKT06）
摘要

为解决涉枪物证检验鉴定中大批量气枪弹的计数问题,参照文献报道中有关称重计数的计算方法,建立气枪弹称重计数的方法。使用天平对气枪弹总质量进行称量,并从气枪弹中随机抽取2批各10发称量计算单发气枪弹质量,将总质量与单发气枪弹质量的商作为气枪弹数量,并将两次抽样称重的误差进行取合。从鉴定实际需要的角度,对称重计数法的可行性进行验证与讨论,并建立气枪弹称重计数的操作流程。

关键词: 物证鉴定; 称重计数法; 气枪弹; 涉枪案件
中图分类号:DF794.1 文献标志码:A 文章编号:1008-3650(2018)06-0436-05
Weighing to Count the Quantity of Air Gun Pellets
BAO Liyin1, LI Yiyi1, ZHANG Wen2, CUI Bin1,*, JIN Yifeng1, MA Xinhe1
1. Institute of Forensic Science, Ministry of Public Security, Beijing 100038, China
2. College of Environment and Chemistry Engineering, Yanshan University, Qinhuangdao 066004, Hebei, China
Abstract

Quantity determination is sometimes crucial for the gun-concerned evidence identification when a large amount of air-gun pellets are involved. Referred to the literature reports about quantity calculation by weighing and counting, a method is here set up for counting air-gun pellets through weighing. The total mass of air-gun pellets is weighed with an eligible electronic balance. Two batches of samples are randomly selected to have their respective 10 air-gun pellets measured so as to get the average weight of one air-gun pellet. The quantity of air gun pellets is calculated through division of the total mass by the average weight of one pellet. The error is also estimated through combination of the results from the two batches of randomly selected samples. Orienting to the actual requirements of identification, the above method is verified and discussed on its feasibility along with the operational procedure being put up, plus the three ways of result-expression being shown with either the pellet amount or the error range or the quantity span.

Key words: evidence identification; weighing and counting; air-gun pellet; gun-involved crime

当前的涉枪刑事案件中, 涉及气枪弹的案情屡见报道[1, 2, 3]。非法制造、买卖、运输、邮寄、储存气枪弹的起刑点为500发, 非法持有、私藏气枪弹的起刑点为1000发。因此一旦触及刑法, 涉案气枪弹的数量往往较多, 从数百至数十万发不等。常见气枪弹体积小、质量有限, 对其进行人工清点计数, 不仅耗时耗力, 而且容易产生误差。一旦气枪弹的数量达到数千以上, 人工计数即陷入困境。解决这一问题, 目前有两种思路, 一是借用工业生产中的自动计数设备[4], 对气枪弹检材进行逐一计数。这种方法在理论上可行, 但需要进行进一步的仪器设备调试与研发工作, 其清点速度与进度有待检验; 而且可以预测的是, 自动计数设备的投入使用需要鉴定机构付出一定设备成本。另一种是通过称重计数的方法, 称量气枪弹检材的总质量, 并通过称量小批量气枪弹获取单发气枪弹的质量, 总质量除以单发气枪弹质量, 即得到气枪弹检材的数量。称重计数仅需量程适合的电子秤, 设备要求简单, 但需解决计数误差的验证问题, 并获得司法裁判过程的采信。当前的非法制造气枪弹裁判案例中, 经过珠海市中级人民法院一审和广东省高级人民法院二审的一起案件值得关注[5, 6]。两级法院均采信了对于多类气枪弹的鉴定意见, 并认可公安机关在鉴定的基础上, 通过称重计数的方式清点多类气枪弹数量的做法, 最终认定的气枪弹总数超过40万。数十万的气枪弹, 通过人工清点几乎难以完成, 而且人工清点误差难以估计。因此, 借助称重计数, 对于巨量气枪弹进行清点, 成为公、检、法各方在这一案例中, 不得不选用、采信的方式, 裁判文书中未见被告方对称重计数方式提出的异议和辩解。

称重计数在工业生产中的零件计数和硬币计数上均有应用, 但这方面的研究报道大多较为简略[7, 8]。陈宝琛等人在较早的一篇论文中, 详细论证称重计数的合理性, 给出误差控制和估测单个物体质量的方法[9]。论文中提出的称重计数规范与误差估计方法, 可以成为气枪弹称重计数的理论基础和基本方案。批量生产的零件依靠夹具或模具控制尺寸, 因此其质量虽存在偏差且为随机变量, 但其偏差服从正态分布。基于此, 陈宝琛等人从生产过程中需要解决的小零件人工点数问题出发, 以数理统计理论分析讨论每次称重的零件数和称重范围[9]。气枪弹的尺寸、质量均类似于工业生产中的小零件, 而且即使是非法生产的非制式气枪弹, 也都是由模具模压而来。因此, 将气枪弹类同于小零件, 认为其质量近似服从正态分布, 使用类似的称重计数规范, 是有其合理性的。基于陈宝琛的研究报道, 本文随后对实验原理与方案设计进行介绍。

1 实验
1.1 原理

当需要称重计数的气枪弹检材总质量为M时, 设气枪弹样本单发质量均值为G, 则气枪弹检材总数量N为：

N=$\frac{M}{G}$（1）

设样本标准差为σ , 可以得出气枪弹临界数量N0为：

（2）

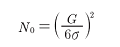
当N≤ N0时, 可以认为, 气枪弹检材的数量为N, 正态分布下其概率为99.7%, 误差极小[9]。

样本标准差的计算公式为：

（3）

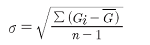
其中Gi为样本中每个气枪弹检材的质量, 为样本中气枪弹检材质量均值, n为样本量。

实际案件中, 虽然有尽量精确地获取气枪弹数量的需要, 但实际上除了涉及定罪量刑的特定数量附近以外, 对于气枪弹数量的计数值, 是可以容许有一定的误差范围的, 只要计数结果和误差范围区间都落在某些特定数量（如500、1000等）的同侧即可。当(A-1)2N0< N≤ A2N0时, 气枪弹检材的数量可以精确到N± (A-1); 当A2N0< N≤ (A+1)2N0时, 气枪弹检材的数量可以精确到N± A。A的数值即是气枪弹称重计数过程中可以容许的误差范围。本文还会使用相对极差这一概念, 相对极差r通过以下公式计算

（4）

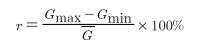
其中Gmax为样本中气枪弹检材质量最大值, Gmin为样本中气枪弹检材质量最小值, 为样本质量均值。

1.2 实验设计

基于气枪弹检材数量可以允许一定程度误差范围的前提条件, 实验设计旨在寻找一个适合的样本量, 用于估计单发气枪弹的质量, 并将真实逐发点数的气枪弹数量与称重计数的结果相比较, 观察真实数量是否落在称重计数值的误差区间内。样本量n和适合的误差范围A是通过实验应当确定的两个主要内容。样本数量不能过多, 否则增加通过称量样本估计气枪弹单发质量的工作量, 使得称重计数简化检验过程的效果不显著; 也不能过少, 否则将导致估计的气枪弹单发平均质量和样本标准差偏离整体平均值过多, 使得气枪弹检材真实数量与称重计数得到的结果相去甚远, 称重计数不能反映真实数量。

尽管气枪弹中的非制式种类, 也是主要来源于模具压制生产方式, 但毕竟不完全等同于工业生产, 其质量分布在类似于正态分布的基础上, 依然可能存在偏差, 所以误差范围同样需要经过实验确认。通过对真实案件中的气枪弹进行称量, 在确定的样本量条件下, 得出相应的误差临界数量N0, 并通过真实数量与称重计数值的差距, 得出适合的误差A。需称重计数的气枪弹数量一般从1000左右开始, 在此基础上, 由样本量n为10始, 进行多组样本的抽取和平均质量计算。以误差A≤ 10为目标, 对多组气枪弹检材进行逐发计数和称重计数, 得出真实数量Nr与称重计数值N, 进行比较与讨论。

1.3 称量工具

对气枪弹总质量的称量使用上海友声衡器有限公司生产的BT-3000型电子天平, 最大称量3 kg, 最小分度值0.1 g。对单发气枪弹质量的称量, 使用奥豪斯仪器（OHAUS）生产的AR153CN型电子天平, 最大称量151 g, 最小分度值0.001 g。

1.4 实验对象

选取实际案件中的3批气枪弹检材进行称重计数。3批气枪弹质量、形状均有一定差异, 经鉴定均为非制式气枪弹, 即并非正式生产厂家生产制造, 有可能为违法犯罪人员自行模压制造。各批气枪弹数量均经过逐个点数, 得出准确数量860发、895发、1057发, 用于和称重计数的结果进行比较, 得到称重计数的误差值。

2 结果与讨论
2.1 气枪弹的称重计数检验

经过逐个计数的860发气枪弹, 称量其总质量为1166.0 g。从中随机抽取100发气枪弹, 按照抽取顺序编为10组, 每组10发气枪弹, 进行逐一称量获取每发质量, 数据见表1。将总质量除以各组均值, 得到以每组10发气枪弹平均质量计算的气枪弹数量N, 作为各组的称重计数结果, 与真实数量860比较得出误差δ ; 计算各组的均值G、标准差σ 、相对极差r、临界数量N0和以允许最大误差为10的条件得出的临界数量倍值(10+1)2N0, 列于表2。

表1 860发气枪弹中随机抽取100发的逐发质量(g) Table 1 Weight (g) of single one air-gun pellet out of 100 ones randomly selected from 860 pellets
表2 860发气枪弹的称重计数统计数据 Table 2 Statistical data by weighing to count 860 air-gun pellets

表2列出的称重计数值N与真实数量860或多或少都存在误差, 由于设计实验的初衷是希望获取误差少于± 10的称重计数方法, 故当称重计数值N≤ (10+1)2N0时, 认为本组抽样得出结果的预期误差是不超过± 10的。表2中仅有第8组不满足N≤ (10+1)2N0, 因此本组抽样结果舍去, 实际上这组的称重计数值为893, 与真实数量的误差高达33, 也是误差较大应当放弃的。剩余的各组中, 存在N≤ (10+1)2N0, 但误差的绝对值超过10的情况, 与陈宝琛等人的研究不相符[9]。原因在于, 实际案件中的非制式气枪弹, 虽然大体上服从正态分布, 但依然会出现质量随机变化的情况, 导致部分抽样组出现偏差。因此, 需要通过进一步筛选, 舍去明显不合理的抽样组, 保证通过抽样得出的平均质量, 能够使真实数量落在称重计数值及其误差范围内, 即N-10≤ 860≤ N+10。

误差超出范围的第1和第4组, 其相对极差明显过大, 已经被排除的第8组, 相对极差也很大。如果将相对极差超过15%的抽样组都舍去, 则剩下7组都能满足使真实值落在称重计数值± 10的误差范围内的要求。这种相对极差较大的情况, 实际从表1的称量数据中能够部分观察到, 第1、第4、第8组都出现某个气枪弹质量偏大或者偏小的情况, 特别是相对极差最大的第8组, 第5发气枪弹质量显著偏小。除了极差之外, 标准差也可以用于描述某组样本的偏差问题, 但由于临界数量值N0已经包含了标准差σ 作为运算因子, 不宜再重复使用标准差进行样本筛选。由此可以初步得出称重计数的方案, 即随机抽取10发样本, 通过逐个称量记录其质量。如果没有出现明显偏重或偏轻的气枪弹, 则计算10发气枪弹质量的平均值。通过气枪弹全体的总质量与样本质量的商, 得出气枪弹数量的称重计数值N, 并认为真实数量大概率地落在N± 10的范围内。这一方案的可行性, 是否需要对样本相对极差、标准差、(10+1)2N0等数据进行计算, 验证抽样样本的可靠性, 抽样的组数, 遇到不合格抽样样本时的处理方式, 需要通过更多非制式气枪弹检材的称量计数进行验证。

2.2 气枪弹的称重计数结果验证

对经过逐个计数确认的895发和1057发气枪弹检材, 重复2.1中所描述的各随机抽取10组共100发气枪弹并逐个称量的过程。逐发称量的质量不再一一列出, 直接通过表3和表4展示称量后的各随机抽样组统计数据。

表3 895发气枪弹的称重计数统计数据 Table 3 Statistical data by weighing to count 895 air-gun pellets
表4 1057发气枪弹的称重计数统计数据 Table 4 Statistical data by weighing to count 1057 air-gun pellets

对895发气枪弹进行称重计数, 虽然大部分抽样组得出的N与真实值895的误差较小, 但依然有3组出现大于10的情况, 而且误差较大的这几组抽样样本的相对极差均小于15%, (10+1)2N0也远大于称重计数值N。相似的结果在1057发气枪弹的称重计数中也有出现, 经过(10+1)2N0< N和相对极差大于15%排除第2组样本之后, 依然存在第7组样本误差为11, 大于10的情况。

上述两次实验, 可靠性检验指标均未能筛选排除误差略超过± 10的情况, 这说明实际案件中的非制式气枪弹, 是有可能出现因为质量分布不完全服从正态分布, 而导致称重计数的误差较理论估计值更大的情况。为了减小这种称量样本不稳定导致的数量估计误差, 保证称重计数的准确程度, 必须找到可靠、简便的处理方法。

2.3 样本量与误差范围

控制误差最直接方式是增加抽样数量, 将每组样本10发增加到15、20或者更多。但是, 增加样本数会增加抽样过程和统计计算的工作量; 而且, 使用以正态分布为基础的统计公式, 单纯增加样本数, 并不能保证抽样结果能满足正态分布条件下提出的误差要求。为实现气枪弹称重计数误差的可控, 不如采用增加抽样组数, 称重计数值取均值, 并将多组误差取并集, 主动扩大误差范围的做法, 这样真实数量落在扩大了的确定的误差范围内的概率将随之增大。由于误差绝对值超过10的情况虽有发生, 但都超出不多, 显示非制式气枪弹偏离正态分布的程度并不显著。选择增加1组抽样称重样本, 抽样2组, 每组10发。如果出现相对极差过大, 即某发气枪弹显著偏轻或偏重的情况, 则舍去该组, 重新抽样1组。此时获取的样本, 应都能满足相对极差小于15％, 和临界数量倍值(10+1)2N0≥ N的要求。样本增加1组, 将显著提高抽样估计单发质量的准确性, 其误差范围将以更大概率涵盖真实值。将两组样本的称重计数值N取平均, 两组样本按照± 10的误差范围取并集, 可以极大提高真实值落在称重计数值及其误差范围内的概率。以表2的第2、第3组样本为例, 称重计数值可表示为863, 即870与855的均值, 误差范围为[845, 880], 经检验, 真实值860落在误差区间中。

表2、3、4中满足极差和临界数量倍值要求的随机样本各有7、9、10组, 表内两两组合共有102组, 基本都满足使真实数量落在± 10的误差范围内的要求。仅有表3中的第2组和第10组组合后误差为-11, 存在超过± 10的情况。这种2组组合后误差仍超出范围在102组随机组合中仅出现1例, 比例小于1％, 且其均值超出预定误差范围很小, 是可以接受的。表3的第1组和第2组, 第1组和第10组组合后会出现误差区间的并集不连续的情况, 如[874, 894][896, 916]。对于这种不连续区间, 即使再抽取例如表3中的第3组这种满足可靠性的样本, 其称重计数值和误差范围的作用, 也仅仅是将不连续区间连贯起来, 因此, 对于不连续区间, 直接将两段区间中的部分连贯起来即可。表3的第1组和第2组称重计数值即为895, 误差范围为[874, 916], 经检验, 真实值895落在误差区间中。

3 称重计数计算气枪弹数量步骤

面对数百至数千的气枪弹检材时, 称重计数可以实现对数量的估算, 并将误差控制在一定范围内。称重计数的总质量通过适合量程的量器获取; 单发气枪弹的质量通过随机抽样称量计算获取。

随机抽取两批各10发气枪弹检材, 逐发称量质量, 统计两组各自的质量均值G、标准差σ 和相对极差r, 通过式（1）计算称重计数值N, 通过式（2）计算N0值。要求两组抽样检材均满足相对极差r≤ 15％和N≤ (10+1)2N0, 如不满足, 则重新进行抽样1~2次。如依然不能获得可靠的抽样样本, 则应考虑增加抽样数量, 或检材本身质量不稳定不适合直接称重计数。对抽取的两组可靠样本的称重计数值N1, N2取平均, 并将两组样本的误差范围[N1-10, N1+10], [N2-10, N2+10]取并集; 若并集不连续, 则将误差区间表示为从两组样本误差范围最小值到最大值的连续区间, 最终得出称重计数值N, 与误差范围[X, Y]。

4 称重计数法的结果应用

称重计数法计算气枪弹的目的在于, 减少计算此类轻小均匀检材时的工作量, 并将计算结果的误差控制在可以接受的范围内。因此, 尽管本文已经提出了称重计数的步骤和结果表达方式, 但其应用仍然可以结合鉴定实际需要, 有多种形式可供参考。

第一种形式, 由于已经得出称重计数值和误差范围, 可以直接使用称重计数值作为气枪弹的检材数量, 并在需要的情况下将误差范围加以标注。此类方式能够最直接地解决气枪弹的数量问题, 给出确定性较强的检材数目N, 并提供一个有明确范围的误差区间[X, Y]。当误差区间跨过关键数值的时候, 则需要对检材进行精度更高的计数。

第二种形式, 如果称重计数值及误差区间, 都落在某些关键数值的同侧, 则可以使用气枪弹检材数量居于X与Y之间的说法, 即不表达具体数量, 以误差区间范围作为气枪弹检材的数量范围。这样的表达方式, 可以避免确定性数值可能带来的争议, 但也可能导致未给出具体数值而使检材数量不明确。

第三种形式, 既然涉及气枪弹定罪量刑有一系列关键数量, 而且在大批量气枪弹抽样检验时, 也有不同数量区间下的不同抽样方案。那么, 如果称重计数误差范围始终落在这些数量形成的区间内, 则可以用关键数量形成的区间描述气枪弹的数量, 如气枪弹检材数量介于1000~1200之间等表达方式。这种方式能够最大程度明确气枪弹检材数量所处的范围, 并与后续检验操作、鉴定意见的应用获得关联; 其不足之处在于, 没有对气枪弹检材进行数量或者数量范围上的任何描述, 仅根据鉴定需要划分其数量所居的区间。

上述研究均基于数百至数千范围内的气枪弹称重计数, 如果面对数量级更高, 数万乃至数百万气枪弹需要计数时, 应适当增大抽样获取质量均值的样本量, 样本量的增加倍数可参考检材数量, 成比例进行增加。

本文所报道的气枪弹数量统计的称重计数法, 可应用于各类轻小、均一的检材计数。参照前人的研究成果, 对各类枪弹、小型枪支散件的计数, 在经过实际验证后, 是可以使用称重计数方法计算数量的。

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。The authors have declared that no competing interests exist.

参考文献
[1] 山东省高青县人民法院. (2016)鲁0322刑初63号刑事判决书[EB/OL]. [2016-08-22]. http://wenshu.court.gov.cn. [本文引用:1]
[2] 广东省连州市人民法院. (2016)粤1882刑初46号刑事判决书[EB/OL]. [2017-02-09]. http://wenshu.court.gov.cn. [本文引用:1]
[3] 安徽省和县人民法院. (2016)皖0523刑初65号刑事判决书[EB/OL]. [2016-05-31]. http://wenshu.court.gov.cn. [本文引用:1]
[4] 赵群英. 一种螺母点数机: CN 105857654 A[P]. 2016-08-17. [本文引用:1]
[5] 广东省珠海市中级人民法院. (2013)珠中法刑初字第12号刑事判决书[EB/OL]. [2014-02-26]. http://wenshu.court.gov.cn. [本文引用:1]
[6] 广东省高级人民法院. (2013)粤高法刑三终字第239号刑事裁定书[EB/OL]. [2014-01-06]. http://wenshu.court.gov.cn. [本文引用:1]
[7] 吴建国. 称重法在计数收发中的妙用[J]. 中国计量, 1998(3): 27-28. [本文引用:1]
[8] 詹姆斯•戴根. 硬物计数变得更容易[J]. 衡器, 2001, 30(1): 36-41. [本文引用:1]
[9] 陈宝琛, 邓定邦. 称重计数法合理计量规范的探讨[J]. 江苏工学院学报, 1987, 8(3): 57-64. [本文引用:4]