本实验样品收集了市场常见品牌（大众、本田、丰田、奇瑞、奥迪、现代、福特、比亚迪、雪铁龙、标致、夏利、尼桑等）轿车不同部位的玻璃, 其中后视镜玻璃57种、灯罩玻璃17种、风挡玻璃63种、车窗玻璃17种。覆盖市场常见轿车品牌的玻璃种类60%以上。收集了常见日用玻璃46种, 其中包括温度计玻璃、容器玻璃等。收集样品共计200种。

仪器：Newwave UP213固体激光器, Agilent 7500a 型四极杆电感耦合等离子体质谱仪。仪器工作参数见表1。

表1

Table 1

表1(Table 1)

表1 LA-ICP/MS工作条件及参数 Table 1 Working conditions and parameters of LA-ICP/MS 激光工作参数 ICP/MS工作参数 激光工作模式 Q-switched 入射功率 1300W 激光能量 50%~80% 采样深度 6.5mm 脉冲频率 10 Hz 采样锥孔径 1.0mm 剥蚀池气体及流速 Ar 1.20~1.40 L· min-1 截取锥孔径 0.4mm 剥蚀方式 线扫描 信号采集方式 时间分辨（TRA） 剥蚀孔径 100 μ m

表1 LA-ICP/MS工作条件及参数 Table 1 Working conditions and parameters of LA-ICP/MS

电感耦合等离子体质谱法可同时测定多种元素^{[3, 4, 5]}, 本实验用LA-ICP/MS对玻璃样品进行检验^{[6, 7, 8, 9]}, 根据玻璃中元素浓度分布的特点和元素的稳定性等因素, 筛选出元素共42种, 将它们的浓度数据作为每个玻璃样品的基础数据, 表2为部分样品数据。

表2

Table 2

表2(Table 2)

表2 部分样品数据 Table 2 Partial sample data (µ g/g) 样品 118Sn 197Au 7Li 9Be 11B 24 Mg 27Al 奇瑞A5前风挡1-1 447.9 0.003811 3.521 0.1584 7.05 20970 7180 奇瑞A5前风挡1-2 137.5 0.005248 3.749 0.1632 7.309 20530 6986 奇瑞A5前风挡1-3 116 0.003181 3.68 0.1986 7.286 20520 6935 奇瑞A5前风挡1-4 55.78 0.003783 3.474 0.1424 7.467 20910 7099 奇瑞A5前风挡1-5 101.4 0.004144 3.566 0.127 7.161 20550 6747 夏利前风挡1-1 4.896 0.004281 3.895 0.1575 7.016 22650 6180 夏利前风挡1-2 4.569 0.003357 3.867 0.1382 6.958 22140 5743 夏利前风挡1-3 4.698 0.003057 3.838 0.1502 7.23 22000 5624 夏利前风挡1-4 34.5 0.003523 3.864 0.1549 7.159 20590 5641 夏利前风挡1-5 75.02 0.003784 3.976 0.1518 7.58 20520 5316 别克赛欧前风挡1-1 148.4 0.001832 7.015 0.2402 4.811 26240 5556 别克赛欧前风挡1-2 137.7 0.00249 7.078 0.2212 5.019 25300 5384 别克赛欧前风挡1-3 128.3 0.002394 6.707 0.2306 5.216 24930 5132 别克赛欧前风挡1-4 7.56 0.002531 6.725 0.2221 4.889 23050 5842 别克赛欧前风挡1-5 7.473 0.004667 7.546 0.2486 4.882 23010 5733 公交车车窗1-1 4.749 0.06872 3.418 0.2136 13.82 16210 149.8 公交车车窗1-2 5.095 0.04811 3.427 0.1996 13.77 16050 146.7 公交车车窗1-3 904.7 0.04956 5.882 0.4071 19.64 16560 150.6 公交车车窗1-4 4.562 0.07117 3.664 0.2143 14.05 16810 153.3 公交车车窗1-5 4.512 0.05661 3.826 0.2949 14.32 16590 151.2 陈世家五粮老陈醋1-1 62.37 0.02647 553.7 12.89 113.7 1049 8964 陈世家五粮老陈醋1-2 63.93 0.0114 559.4 12.86 116.8 1098 9175 陈世家五粮老陈醋1-3 66.7 0.01737 526.9 12.41 117 1083 8899 陈世家五粮老陈醋1-4 1298 0.01361 545.6 12 115.6 1095 8465 陈世家五粮老陈醋1-5 63.88 0.01013 548.8 12.14 116.4 1099 8754

表2 部分样品数据 Table 2 Partial sample data (µ g/g)

激光剥蚀方式采用线扫描, 采样流程如下：预剥蚀(10 s)除去表层污染, 其后依次为载气冲洗(10 s)、激光预热(10 s)、样品剥蚀(70 s)、载气冲洗(10 s)等步骤。玻璃样品分析采用NIST612为外标, 29Si为内标元素来消除基体效应和激光剥蚀效率变化等因素。

对每种玻璃样品进行不少于10次测试, 得到的数据通过STDEV函数计算标准偏差。STDEV函数能够反映数值相对于样品平均值的离散程度, 通过该函数剔除偏离样品均值较大的测试数据, 保留7组有效数据。该检验方法能够采集到大量的元素, 但是如果将一些不稳定元素也纳入数据库, 在进行统计比对计算时反而会使目标数据偏离其应该归属的种类, 因此应先根据样品性质选择合适的元素。在元素选择时主要考虑到以下因素：

1）仪器空白数据中本底值较高的元素, 如P。

2）各样品中含量差异不大的元素, 如Au、Cd。

在表2中可以看到Au在各种玻璃样品中元素浓度差异小, 区分度不明显, 应剔除, 同理剔除Cd。

3）在样品重复测试中浓度不稳定的元素, 如Cu、Tl、Sn。Sn在大部分玻璃样品中均出现浓度不稳定的数据, 重复测定浓度差异大, 应剔除, 同理剔除Tl和Cu。

将以上干扰较大及不稳定的元素去除, 最终得到玻璃中元素共42种：Li、Be、B、Mg、K、Sc、Ti、V、Cr、Mn、Fe、Co、Ni、Zn、Ga、Rb、Sr、Y、Zr、Nb、Mo、Cs、Ba、La、Ce、Pr、Nd、Sm、Eu、Gd、Tb、Dy、Ho、Er、Tm、Yb、Hf、Ta、W、Pb、Th、U。

通过对不同玻璃中的42种元素浓度数据进行分析, 确定不同种类玻璃的元素浓度存在差异, 利用此差异, 可以将不同的玻璃样品区分开来。

在7组数据中随机挑选5组, 建立基本的样品数据库, 并对样品数据进行统一编码。将剩下的2组数据放于测试数据库中。通过建立样品数据集和测试数据集对统计比对算法进行测试, 以期选出最有效的算法。

本实验中使用距离判别的方法确定测试数据和样品数据是否同一。距离是科学研究与工程技术领域中使用非常广泛的一种度量, 通常被用作衡量两个个体间的相似性^[10]。距离判别分析方法是判别样品所属类别的一种应用性很强的多因素决策方法, 根据已掌握的、历史上每个类别的若干样品数据信息, 总结出客观事物分类的规律性, 建立判别准则, 当遇到新的样品点, 只需根据总结得出的判别公式和判别准则, 就能判别该样品点所属的类别。距离判别分析的基本思想是：样品和哪个总体的距离最近, 就判它属于哪个总体。

本实验通过对多种距离判别方法进行测试比对, 选择马氏距离作为主要的判别方法。马氏距离由印度数学家马哈拉诺比斯(Mahalanobis)首先提出, 所以又称为Mahalanobis Distance, 是一种采用协方差来计算两点之间距离的方法。它是一种有效的计算两个未知样品集相似度的方法。马氏距离是多元统计中常用的一种判别方法。马氏距离的定义如下：

定义1：设x, y是从均值向量为μ , 协方差阵为∑ 的总体g中抽取的两个样品, 定义x, y两点之间的马氏距离为：

\[d^2_m(x, y)=(x-y)’ \sum^{-1}(x-y)\]

定义2：x与总体g的马氏距离为：

\[d^2_m(x, g)=(x-\mu)’ \sum^{-1}(x-\mu)\]

马氏距离是建立在协方差的基础上, 它不受量纲的影响, 两点之间的马氏距离与原始数据的测量单位无关; 由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。马氏距离的优点在于它将协方差作为距离计算的一项因子, 提高了多维向量距离计算的准确度, 但也因为马氏距离增加了协方差的运算, 算法本身的难度也加大。

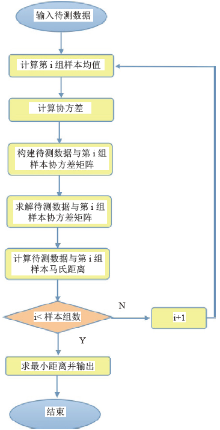
马氏距离算法实现的流程图见图1。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 马氏距离算法实现的流程图Fig.1 Flow chart by Mahalanobis distance algorithm